数据结构 Heap 堆

回顾：完全二叉树

若设二叉树的深度为h，除第 h 层外，其它各层（1～h-1）的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树（Complete Binary Tree）。

满足下列性质：

1、只允许最后一层有空缺结点且空缺在右边，即叶子节点只能在层次最大的两层上出现； 2、对任一节点，如果其右子树的深度为 j，则其左子树的深度必为 j 或 j+1。即度为 1 的点只有 1 个或 0 个； 3、除最后一层，第 i 层的节点数是：2i−1； 4、有 n 个节点的完全二叉树，其深度为: $log2n+1$ 或为 $log2n+1$ ； 5、满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

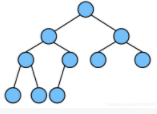
注意：最下面一层一定是从左往右逐步变满的

所以下面这种不是完全二叉树

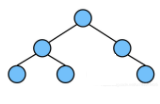
基于上面那个性质，完全二叉树可以使用数组来表示：

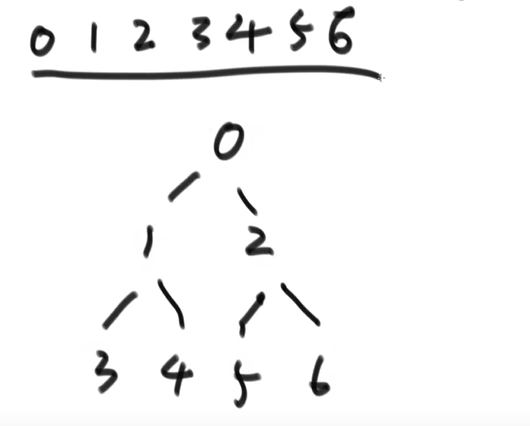
基于此可以直接计算下标的位置：

左：2 * i + 1
右：2 * i + 2
父：(i - 1) / 2

打印数组完全二叉树的工具

为了方便下面的代码调试，这里提供一个打印数组完全二叉树的工具类

代码参考：gist 地址

[93, 97, 92, 87, 49, 54, 60, 84, 40, 7]

生成效果：

              93                              
            92              
    49      54      60      
40  7  

补充个生成随机数组的工具方法：

/**
 * 生成随机数组
 */
public static int[] generateArray(int len, int max) {
    int[] arr = new int[len];
    for (int i = 0; i < arr.length; i++) {
        arr[i] = (int) (Math.random() * max);
    }
    return arr;
}

堆是什么？

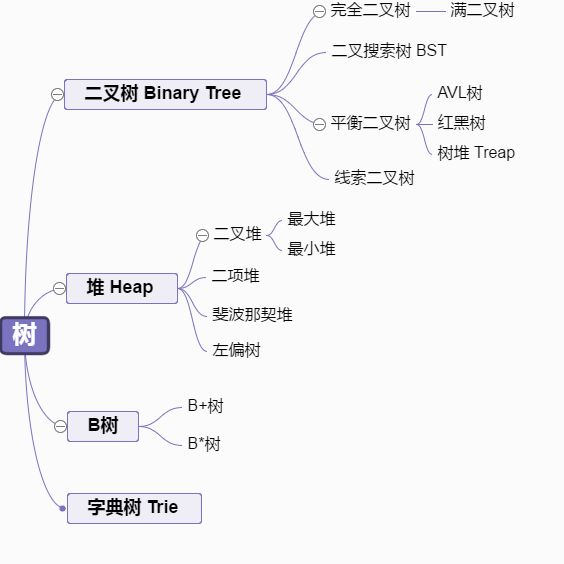
堆是一种特殊的完全树，它每个结点都有一个值，堆的特点是根结点的值最小（或最大），且根结点的两个子树也是一个堆。就类似一堆东西一样，按照由大到小（或由小到大）“堆” 起来。

在最大堆中，父节点的值比每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的 “堆属性”，并且这个属性对堆中的每一个节点都成立。

例子：

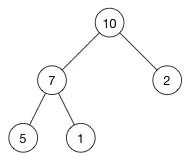
这是一个最大堆，因为每一个父节点的值都比其子节点要大。

来自数组的树

用数组来实现树相关的数据结构也许看起来有点古怪，但是它在时间和空间上都是很高效的。

我们准备将上面例子中的树这样存储：

[ 10, 7, 2, 5, 1 ]

就这么多！我们除了一个简单的数组以外，不需要任何额外的空间。

如果我们不允许使用指针，那么我们怎么知道哪一个节点是父节点，哪一个节点是它的子节点呢？问得好！节点在数组中的位置 index 和它的父节点以及子节点的索引之间有一个映射关系。

如果 i 是节点的索引，那么下面的公式就给出了它的父节点和子节点在数组中的位置：

parent(i) = floor((i - 1)/2)
left(i)   = 2i + 1
right(i)  = 2i + 2

注意 right(i) 就是简单的 left(i) + 1。左右节点总是处于相邻的位置。

堆和普通树的区别

堆并不能取代二叉搜索树，它们之间有相似之处也有一些不同。我们来看一下两者的主要差别：

节点的顺序：在二叉搜索树中，左子节点必须比父节点小，右子节点必须必比父节点大。但是在堆中并非如此。在最大堆中两个子节点都必须比父节点小，而在最小堆中，它们都必须比父节点大。

内存占用：普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配内存。堆仅仅使用一个数组来存储数据，且不使用指针。

平衡：二叉搜索树必须是 “平衡” 的情况下，其大部分操作的复杂度才能达到 $O(log n)$ 。你可以按任意顺序位置插入/删除数据，或者使用 AVL 树或者红黑树，但是在堆中实际上不需要整棵树都是有序的。我们只需要满足堆属性即可，所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证 $O(log n)$ 的性能。

搜索：在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。

堆这个数据结构有什么好处

堆这个数据结构具有以下好处：

高效的插入和删除操作：堆的插入和删除操作的时间复杂度都是O(logn)，其中n是堆中元素的数量。这是因为堆的结构保证了每个节点的值都大于或等于（或小于或等于）其子节点的值，从而使得插入和删除操作只需要对部分节点进行上浮或下沉操作。
可以高效地找到最大或最小的元素：最大堆可以在常数时间内找到最大的元素，最小堆可以在常数时间内找到最小的元素。这是因为最大堆的根节点就是最大的元素，最小堆的根节点就是最小的元素。
适用于动态数据集的实时更新：由于堆的高效插入和删除操作，它适用于需要实时维护数据集的最大或最小元素的情况。当数据集发生变化时，只需对堆进行相应的插入或删除操作，即可保持堆的性质。
堆排序的应用：堆排序算法是基于堆的一种高效排序算法。它具有稳定的时间复杂度O(nlogn)，且原地排序（不需要额外的存储空间）。堆的特性使得堆排序具有较好的性能，并且在某些场景下优于其他排序算法。

总而言之，堆这个数据结构具有高效的插入和删除操作、快速找到最大或最小元素的能力，以及适用于动态数据集的实时更新等优点。这使得堆在许多算法和数据处理任务中发挥重要作用，如优先队列、图算法、堆排序等。

可以用堆做什么？

堆是一种非常有用的数据结构，它可以应用于多个领域和问题。以下是一些堆的应用示例：

优先队列：堆可以用作实现优先队列的底层数据结构。优先队列是一种特殊的队列，其中每个元素都有一个与之关联的优先级。堆可以维护元素的优先级顺序，使得具有最高优先级的元素能够快速地被访问和删除。
求TOP-K元素：通过使用最大堆或最小堆，可以方便地找到一组数据中的最大或最小的K个元素。堆的插入和删除操作的时间复杂度为O(logn)，使得TOP-K问题可以在较高的效率下解决。
堆排序：堆排序是一种基于堆的排序算法，它利用堆的性质进行排序操作。堆排序具有稳定的时间复杂度O(nlogn)，且原地排序（不需要额外的存储空间）。因此，堆排序在需要高效的排序算法时是一种常用的选择。
图算法：在图算法中，堆常用于实现最短路径算法（如Dijkstra算法和Prim算法）和最小生成树算法（如Prim算法和Kruskal算法）。堆可以用来维护节点之间的权重或距离，并根据特定的优先级选择下一个要处理的节点。
中位数查找：通过使用两个堆（一个最大堆和一个最小堆），可以高效地找到一组数据的中位数。堆可以实时地维护中位数的位置，使得中位数的查找操作具有较好的性能。

除了上述应用外，堆还可以用于解决调度问题、事件处理、数据压缩等许多其他问题。其灵活性和高效性使得堆成为解决各种数据处理和算法问题的强大工具。

堆的实现

数组的堆化 shiftDown

时间复杂度是 $O(log n)$ 。

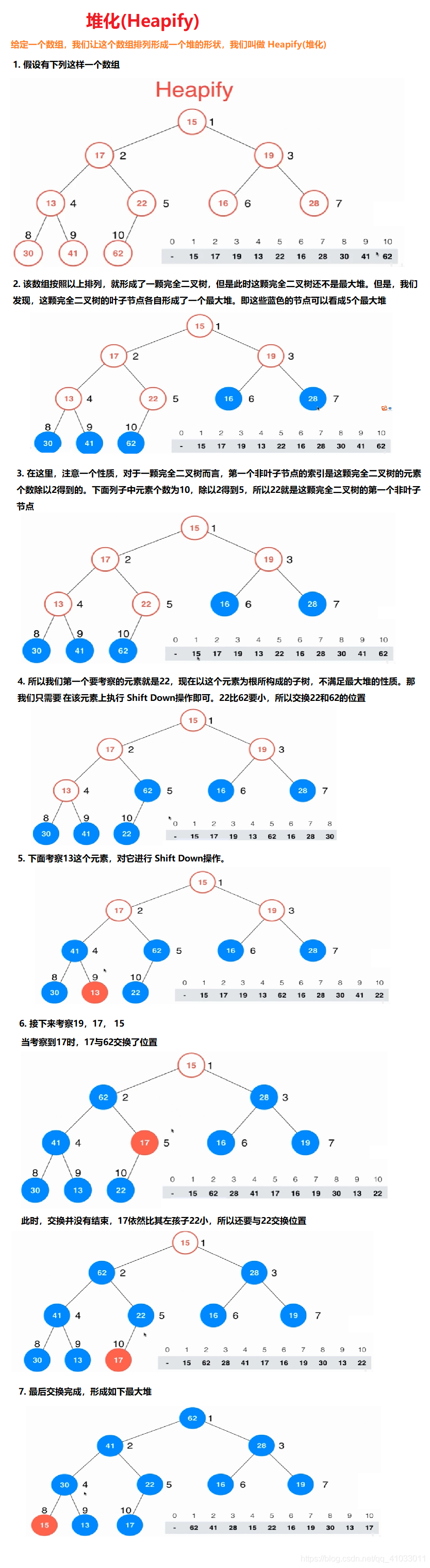
基于此过程编写代码：

/**
 * index 表示要 Shift Down 的位置
 * heapSize 表示堆的大小（因为不是整个数组都是堆，数组可能没有被填满）
 */
public static void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1; // 左孩子的下标
    while (left < heapSize) { // 下方还有孩子的时候
        // 比较两个孩子（左右孩子）谁的值大，把下标给 largest
        int largest = left + 1 < heapSize // 先判断下标有没有越界
                && arr[left + 1] > arr[left] ? left + 1 : left;
        // 父和最大的那个孩子之间，谁的值更大，把下标给 largest
        largest = arr[largest] > arr[index] ? largest : index;
        // 如果相等说明最大值就是这个 index 的节点，因此无需交换了
        if (largest == index) break;
        swap(arr, largest, index);
        // 现在到下面一个节点重复操作
        index = largest;
        left = index * 2 + 1;
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

将普通数组转成堆

利用上面那个堆化函数可以构建出一个堆：

public static void buildHeap(int[] arr) {
    // 将待排序的序列构建成一个大顶堆
    // 这个 arr.length / 2 可以取得完全二叉树的第一个非叶子节点的索引
    for (int i = arr.length / 2; i >= 0; i--) {
        heapify(arr, i, arr.length);
    }
}

测试代码：

public static void main(String[] args) {
    // int[] arr = new int[]{3, 9, 6, 7, 4, 3, 5, 8, 2};
    int[] arr = generateArray(10, 100);
    int[] arrCopy = Arrays.copyOf(arr, arr.length);
    buildHeap(arrCopy);
    System.out.println(Arrays.toString(arr));
    System.out.println(Arrays.toString(arrCopy));

    // 上面提供的工具类
    CompleteBinaryTree.TreeNode root = CompleteBinaryTree.Tool.createTree(arrCopy);
    CompleteBinaryTree.Print.PrintTreeNode(root);
}

打印的结果：

[34, 63, 74, 19, 76, 61, 65, 23, 84, 66]
[84, 76, 74, 63, 66, 61, 65, 23, 19, 34]
              84                              
      76              74              
  63      66      61      65      
23  19  34  

Java 的 PriorityQueue 集合

Java 中的实现类是 PriorityQueue，具体它的细节参考这篇《Java 集合类学习 PriorityQueue》

插入节点 $O(log n)$

我们通过一个插入例子来看看插入操作的细节。我们将数字 16 插入到这个堆中：

堆的数组是： [ 10, 7, 2, 5, 1 ]。

第一股是将新的元素插入到数组的尾部。数组变成：

[ 10, 7, 2, 5, 1, 16 ]

相应的树变成了：

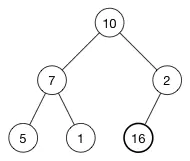
16 被添加最后一行的第一个空位。

不行的是，现在堆属性不满足，因为 2 在 16 的上面，我们需要将大的数字在上面（这是一个最大堆）

为了恢复堆属性，我们需要交换 16 和 2。

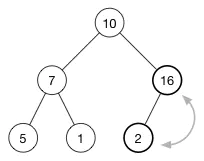
现在还没有完成，因为 10 也比 16 小。我们继续交换我们的插入元素和它的父节点，直到它的父节点比它大或者我们到达树的顶部。这就是所谓的 shift-up，每一次插入操作后都需要进行。它将一个太大或者太小的数字 “浮起” 到树的顶部。（可以直接通过上面的公式计算出节点位置）

最后我们得到的堆：

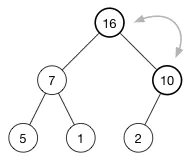
现在每一个父节点都比它的子节点大。

基于此过程编写代码：

public static void heapInsert(int[] arr, int index) {
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        // 检查上一层
        index = (index - 1) / 2;
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

删除根节点 $O(log n)$

下面那个删除任意节点和这个是一样的，所以具体代码就看下面

我们将这个树中的 (10) 删除：

现在顶部有一个空的节点，怎么处理？

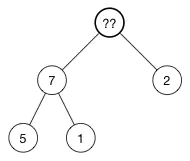
当插入节点的时候，我们将新的值返给数组的尾部。现在我们来做相反的事情：我们取出数组中的最后一个元素，将它放到树的顶部，然后再修复堆属性。

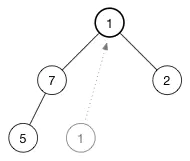
现在来看怎么 shift-down(1)。为了保持最大堆的堆属性，我们需要树的顶部是最大的数据。现在有两个数字可用于交换 7 和 2。我们选择这两者中的较大者称为最大值放在树的顶部，所以交换 7 和 1，现在树变成了：

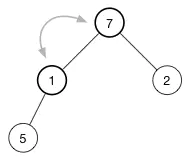
继续堆化直到该节点没有任何子节点或者它比两个子节点都要大为止。对于我们的堆，我们只需要再有一次交换就恢复了堆属性：

删除任意节点

绝大多数时候你需要删除的是堆的根节点，因为这就是堆的设计用途。

但是，删除任意节点也很有用。这是 remove() 的通用版本，它可能会使用到 shiftDown 和 shiftUp。

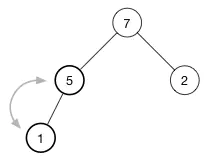
我们还是用前面的例子，删除 (7):

对应的数组是

[ 10, 7, 2, 5, 1 ]

你知道，移除一个元素会破坏最大堆或者最小堆属性。我们需要将删除的元素和最后一个元素交换：

[ 10, 1, 2, 5, 7 ]

最后一个元素就是我们需要返回的元素；然后重复上面删除根节点的操作

扩容的策略

堆在 Java 中扩容是直接原数组长度 * 2，所以插入 n 条元素就需要扩容 $O(logn)$ 次

Reference

堆和树有什么区别？堆为什么要叫堆，不叫树呢？ - Michael Yuan的回答 - 知乎数据结构：堆（Heap）

回顾：完全二叉树​

打印数组完全二叉树的工具​

堆是什么？​

来自数组的树​

堆和普通树的区别​

堆这个数据结构有什么好处​

可以用堆做什么？​

堆的实现​

数组的堆化 shiftDown​

将普通数组转成堆​

Java 的 PriorityQueue 集合​

插入节点 O(logn)O(log n)O(logn)​

删除根节点 O(logn)O(log n)O(logn)​

删除任意节点​

扩容的策略​

Reference​